FEniCSx-Error-Estimation

See all the details in the dedicated publication and the code repository.

What is FEniCSx-EE ?

FEniCSx-EE is an open source library for the finite element software FEniCSx. The goal of this library is to provide an implicit hierarchical a posteriori error estimation method. The method used in FEniCSx-EE has been introduced by R. E. Bank and A. Weiser in this research paper.

The Bank-Weiser estimator

The Bank-Weiser estimator is computed from local solves of Neumann boundary value problems at the level of the mesh cells.

This estimator has several advantages:

It is fully local: its local contributions are based on solutions to Neumann boundary value problems restricted to each cells of the mesh.
It can be adapted to many contexts such as diffusion, reaction-diffusion, convection-diffusion, linear elasticity, Stokes, fractional Laplacian equations.
It is robust: with respect to the coefficient in singularly perturbed reaction-diffusion equations, to the coefficient in convection-dominated convection-diffusion equations and also to linear elasticity in the incompressible limit.
It is flexible: it is possible to vary parameters in the definition of the estimator in order to find the most accurate one.

Details on our algorithm implemented in FEniCSx-EE and examples of applications can be found in the dedicated publication.

The derivation of the Bank-Weiser estimator

We consider the following standard Laplacian equation on a bounded domain with homogeneous Dirichlet boundary condition in weak formulation: we seek $u \in H_{0}^{1} (Ω)$ such that

\begin{matrix} (1) & (\nabla u, \nabla v)_{L^{2} (Ω)} = (f, v)_{L^{2} (Ω)} \forall v \in H_{0}^{1} (Ω) . \end{matrix}

Given a mesh $T$ on $Ω$ and an associated finite element space $V \subset H_{0}^{1} (Ω)$ the finite element discretization of $(14)$ reads: seek $u_{V} \in V$ such that

\begin{matrix} (2) & (\nabla u_{V}, \nabla v)_{L^{2} (Ω)} = (f, v)_{L^{2} (Ω)} \forall v \in V . \end{matrix}

From $(14)$ and $(15)$ we can derive a local equation for the approximation discrepancy given by the function $e := u - u_{V}$ . If we denote $T$ a cell of $T$ , $\partial T$ the set of edges of $T$ and $E$ the edges, the restriction $e_{T} := e_{| T}$ is solution to the following local Neumann problem in weak formulation

\begin{matrix} (3) & (\nabla e_{T}, \nabla v)_{L^{2} (T)} = (r_{T}, v)_{L^{2} (T)} + \frac{1}{2} \sum_{E \in \partial T} (J_{E}, v)_{L^{2} (E)} \forall v \in H_{0}^{1} (Ω), \end{matrix}

where $r_{T}$ and $J_{E}$ are computable functions depending on $f_{V}$ (the $L^{2}$ projection of $f$ onto $V$ ) and $u_{V}$ only.

The core idea of the Bank-Weiser error estimation is to pick a proper space $V^{bw} (T)$ to discretize $(16)$ and obtain a computable function $e_{T}^{bw}$ , solution to

\begin{matrix} (4) & (\nabla e_{T}^{bw}, \nabla v)_{L^{2} (T)} = (r_{T}, v)_{L^{2} (T)} + \frac{1}{2} \sum_{E \in \partial T} (J_{E}, v)_{L^{2} (E)} \forall v \in V^{bw} (T) . \end{matrix}

Note that, since these problems are fully independent from a cell $T$ to another, they can be solved in parallel. Thus, for a given norm, the local finite element error is approached by the Bank-Weiser estimator defined as follow

\begin{matrix} (5) & ‖ e_{T} ‖ ≃ ‖ e_{T}^{bw} ‖ =: η_{T}^{bw} . \end{matrix}

The quantity $η_{T}^{bw}$ can be used to perform adaptive refinement and to approach the global finite element error as follow

\begin{matrix} (6) & ‖ e ‖^{2} ≃ \sum_{T \in T} {η_{T}^{bw}}^{2} . \end{matrix}

In here we develop a new parallel implementation of the Bank-Weiser a posteriori error estimator and we apply it to various problems such as adaptive refinement for standard Laplacian equations with different kinds of boundary conditions, for nearly-incompressible linear elasticity equations and for goal-oriented error estimation.

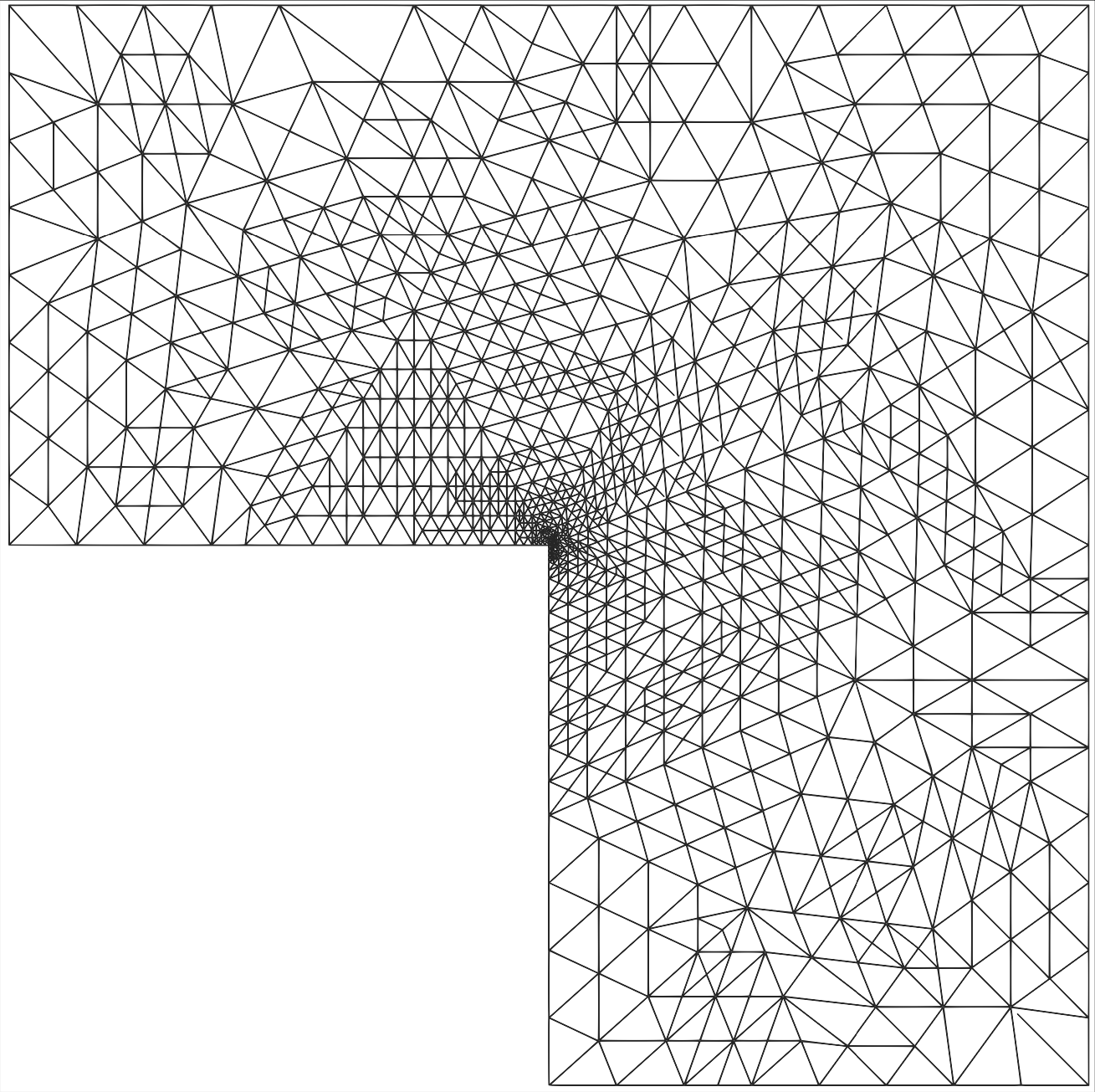
Above are two meshes adapted using the Bank-Weiser estimator. On the left is a standard Laplacian equation on a 2D L-shaped domain. On the right is the mesh of a femur bone on which nearly-incompressible linear elasticity equations are applied. The mesh on the right is adapted with respect to a quantity of interest centered in the middle part of the bone.

Above is the plot showing the strong scaling of our parallel implementation of the Bank-Weiser estimator.

Getting started

To download and get started with FEniCSx-EE, please follow the instructions from the README file on the github repository.

FEniCSx-EE is not currently compatible with the last stable version of FEniCSx. Maintaining FEniCSx-EE is not part of my current position but I try to update it when I find some time. 👷